Madinventions
|
| posted on 17/7/11 at 01:27 AM |
|
|
Another maths / mechanism query...
Ok, this one is making me feel stupid!
 
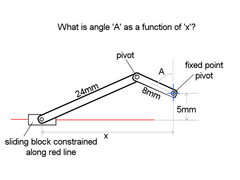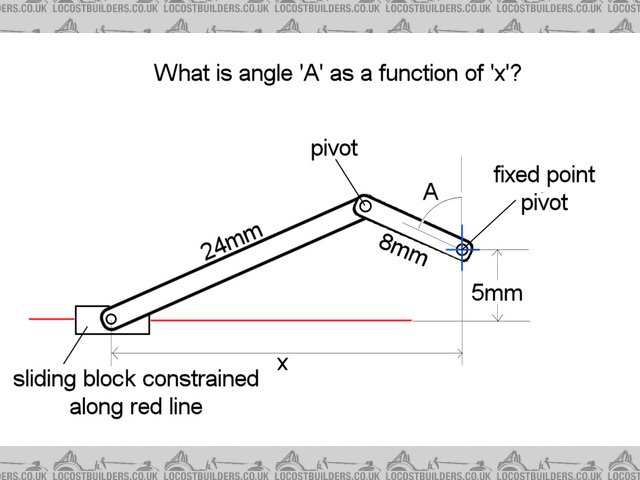
TR mechanism
The sliding block is mounted onto a leadscrew and is moved by a stepper motor. The 'fixed point pivot' cannot move left/right or up.down
but it is free to rotate. What I really need to work out is how to derive the angle 'A' from the position of the block 'x'.
It's been too long since I did any trig and I'm stumped. It's also 2:30am and I'm giving up for the night!
Any help would be much appreciated as always,
Cheers,
Ed.
Mojo build diary: http://www.madinventions.co.uk
Solo music project: Syrrenfor http://www.reverbnation.com/syrrenfor
View my band website:
http://www.shadowlight.org.uk
http://www.eastangliankitcars.co.uk/
|
|
|
|
|
v8kid
|
| posted on 17/7/11 at 06:01 AM |
|
|
The horizontal and vertical distances of the fixed pivot from the mooving pivot ars eassily worked out from sine and cos. That gives the height of the
mooving pivot.
Then use pythagarous to find out how far the sliding block is from the pivot horizontally. Add up horizontal components. Simples!
Easier to do than explain! Now spelling is a different matter 
You'd be surprised how quickly the sales people at B&Q try and assist you after ignoring you for the past 15 minutes when you try and start a
chainsaw
|
|
|
matt_gsxr
|
| posted on 17/7/11 at 07:07 AM |
|
|
Not too easy to actually solve for A because there are some discontinuities from x.
If you follow the method above you get
24 24 = (5 +8 Cos A)(5 + 8 Cos A) + ( x - 8 sin A)(x- 8 sin A)
rearrange
I can't solve for A, but can solve for x,
x = 8 sin A +/- sqrt( 24 24 - 25 - 80 Cos A + Cos A Cos A)
As you notice the +/- as there are 2 solutions for any x.
It might be possible to solve for A, but not by me for free on a Sunday morning!
Matt
|
|
|
v8kid
|
| posted on 17/7/11 at 08:47 AM |
|
|
Don't bother solving it just pop it into excel solver
You'd be surprised how quickly the sales people at B&Q try and assist you after ignoring you for the past 15 minutes when you try and start a
chainsaw
|
|
|
lsdweb
|
| posted on 17/7/11 at 10:06 AM |
|
|
To help, you have 2 reference points where it's easy to calculate x from A using pythag - that is when a = 0 and a = 90 degrees.
Wyn
|
|
|
Madinventions
|
| posted on 17/7/11 at 10:33 AM |
|
|
Calculating X from A is relatively simple, but I needed to calculate A from X... I tried several ways of rearranging the formula to work backwards
but always came up against a bit that couldn't be simplified any further.
However, after a nights sleep it turns out to be a simple scalene triangle with 3 known sides, 24, 8 and 'h' where 'h' is the
hypotenuse of a right angle triangle with length 'x' and height '5'. Pythagoras will work out 'h' and I can then
use the law of cosines to work out the angles in the scalene triangle.  This also simplifies the rather nasty problem of there being 2 solutions of
A for every value of x.
So the moral of the story is: Sometimes it's better to get some distance from a problem and the solution may become clear.
Thanks to everyone for taking the time to think about this for me!
Ed.
Mojo build diary: http://www.madinventions.co.uk
Solo music project: Syrrenfor http://www.reverbnation.com/syrrenfor
View my band website:
http://www.shadowlight.org.uk
http://www.eastangliankitcars.co.uk/
|
|
|
matt_gsxr
|
| posted on 17/7/11 at 10:37 AM |
|
|
so what is the answer then?
show us your formula always keen to learn
|
|
|
