My math skills are adequate, but my verbal skills can be a handicap at times, so please bear with me.
We can say that a square is a special rectangle in that the width and length are equal.
Similarly, we can say that a circle is a special ellipse in that the major axis and minor axis are equal.
Now, if we take a piece of square bar/tube and cut the end off at an angle, the resulting "face" of the bar/tube will be a rectangle. If we
do the same with a round bar/tube, the resulting "face" will be an ellipse.
Here comes the point:
Can we do the reverse? I am pretty sure we can take a piece of rectangular bar/tube and cut it such a manner as to have the resulting
"face" a square. What I am wondering is if we can take a piece of elliptical bar/tube and cut it in the proper manner so the resulting
"face" is a circle?
I asked my father, an engineer (aerospace), and it took nearly an hour to get my question through to him (verbal skills?). Finally, he declared NO!
Cannot be done. I seldom listen to him anyway, so I am asking here.
What do we think?
Dave
no it cannot be done, the angles/lengths can only further diverge.
I get it, but it hurts thinking about it.
Pat...
Not true. If you turn your elipse or rectangle 90 degrees you can cut at an angle such that you stretch its minor axis to match the major axis and
end up with a square or circle again.
Liam
ah yes, but it would match the bigger side of either... fair enough
As i understand it, after the cut, it may look round from a distance, but up close in a position to weld, the face won't be !!
that about right ???? 
Jason
An elipse has a constanly varying radius from the centre point to points on its circumference. A circle has a constant one. By simply cutting the
elipse, you can't make a circle (because of the variable radius. If you can, I cant see how it would work.
David
quick answer!
but, consider this.....
if oriented correctly, the length of the rectangle can remain and the width grows, to point that it equals the length, resulting in a square
"face".
similarly, the major axis of the ellipse can be held fixed, while the minor axis "grows". can't we calculate the proper angle to allow
the minor axis to "grow" equal the major axis, resulting in a circle?
for example, if I have a piece of 4" x 5" tube and cut it at about 53* across the 4" side, the length of the cut will be 5" and
will result in a square "face".
?????
dave
dave
I really agree with Avoneer!
dave
eliptical tube...
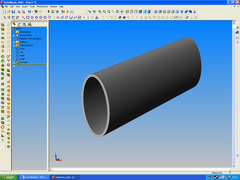
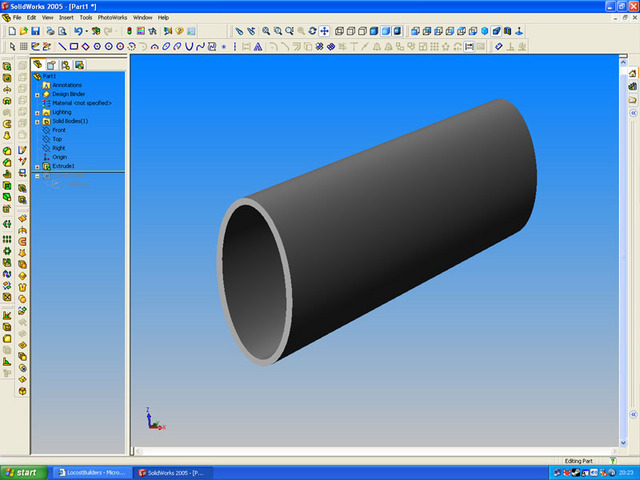
Rescued attachment elipse1.jpg
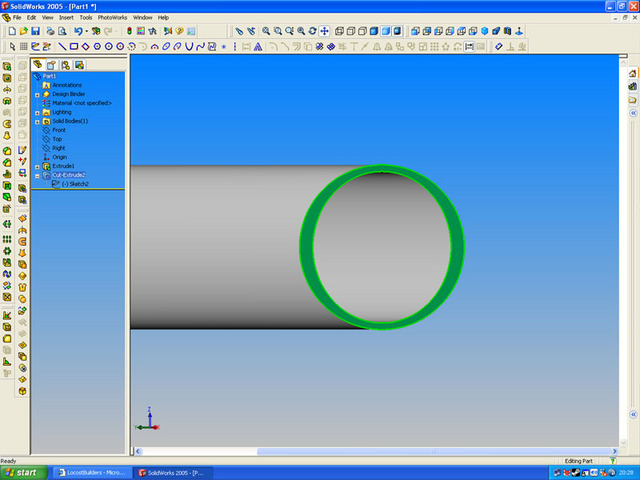
Cut at an angle...
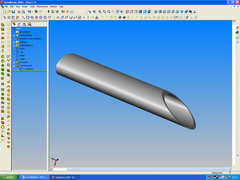
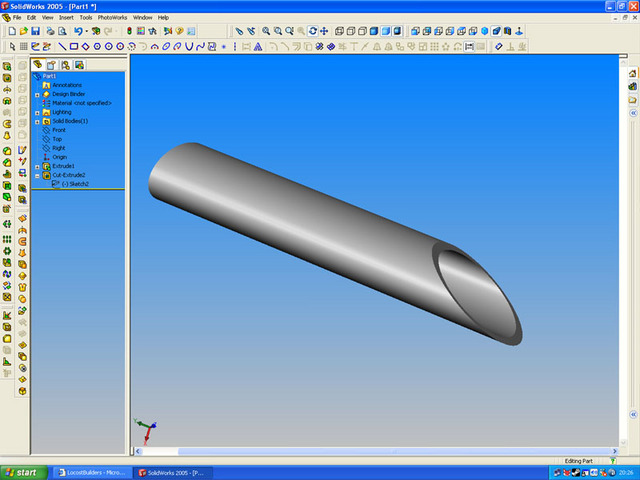
Rescued attachment elipse2.jpg
View of the cut face (normal to it)... Not a perfect circle in this case cos i just guessed the cut angle. Work it out and you can have a perfect
circle...
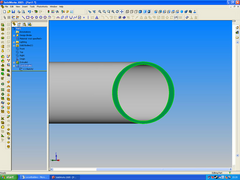
Rescued attachment elipse3.jpg
Ahh. See, now i misunderstood the question.
Haha
David
i'll get my coat
I reckon the angle-of-dangle is:
cos^-1 (a/b) where a is the short side you want longer and b is the long side, that stays the same length.
Looking down on the tube so you see it at its narrowest, the angle is the angle between the end of the tube and the cut, rather than the side of the
tube and the cut.
I did draw a little picture but attaching it was too advanced for me!
keets,
I think you've got my coat, give it back I need it.
quote:
Originally posted by davidcarr
I reckon the angle-of-dangle is:
cos^-1 (a/b) where a is the short side you want longer and b is the long side, that stays the same length.
Looking down on the tube so you see it at its narrowest, the angle is the angle between the end of the tube and the cut, rather than the side of the tube and the cut.
I did draw a little picture but attaching it was too advanced for me!
P.S. To attach a picture from your computer simply click the browse button on the post reply form and find the pic (cant be over 500k or you'll
get an error and loose the essay you might just have typed
). To display a picture from the web use the insert image button in the little tool
bar above the text entry window.
liam
[Edited on 30/1/06 by Liam]
Yes, an eliptical tube, cut ant the correct angle will give a circular "face".
Similarly, a round tube, presented at an angle to the wind, will have an aparent eliptical crossection and so will be more aerodynamic than a round
tube. Good to know when making front wishbones for a seven.
since we've decided it's feasible, can you please tell me why the hell you want to know?
was it purely out of curiosity or are you after doing something with the theory?
tom
The answer is absolutely yes in both cases.
This is quite common in sheet metal ducting that you may see in large buildings for air con or ventilation. The eliptical tube is called an oblique
cylinder and when the end is cut at the correct angle (dependant on the ratio of the ellipse) it will join directly to a round tube, the end of which
is cut at 90 degrees.
The same applies to a rectangular tube which when cut at the appropriate angle will join directly to a square tube the end of which is cut at 90
degrees.
So I agree with Liam etc.
David
That gave me a headache 
But I did understand it!!